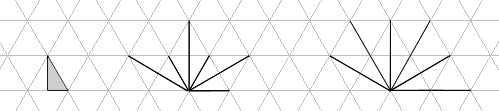
I try to solve this question :
How many convex figures of given area are there ?
The figures should be polygons formed by these types of lines :

The possible figures formed by the first (2nd) type of lines I denote A_n (B_n).
n - is the area of figure, unit (U) is triangle on the picture above.
This choice of possible lines is equivalent to the choice
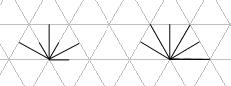
Another possibility is to study convex polydrafters (D_n)
Relations
B_4n < A_n < B_n
A_n < D_n < A_4n
Images
A_2 ![]() A_4
A_4 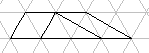

A_6 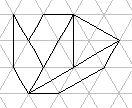 A_8
A_8 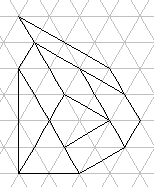 A_8*
A_8*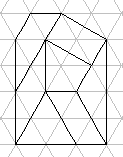
B_6 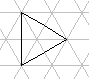 B_8
B_8 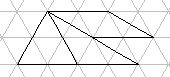 B_12
B_12 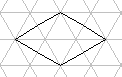
D_2 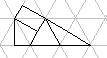 D_3
D_3 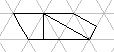 D_4
D_4 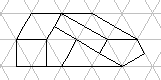
D_5 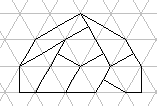 D_6
D_6 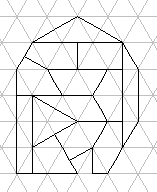
A_8
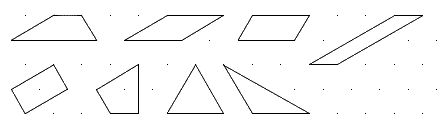
A_12

B_16

D_12
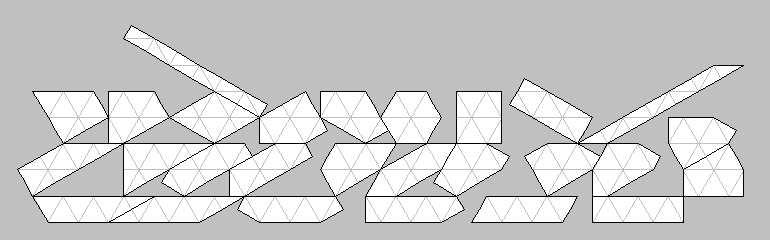
X* is set X without the longest piece
some other images
| n | A_n | B_n | D_n | A_4n | B_4n | B_16n | |
| 1 | 0 | 0 | 1 | 3 | 0 | 6 | |
| 2 | 2 | 0 | 4 | 8 | 3 | 14 | |
| 3 | 0 | 0 | 3 | 11 | 1 | 23 | |
| 4 | 3 | 0 | 7 | 17 | 6 | ||
| 5 | 0 | 0 | 7 | 21 | 0 | ||
| 6 | 5 | 1 | 13 | 31 | 9 | ||
| 7 | 0 | 0 | 9 | 33 | 1 | ||
| 8 | 8 | 3 | 15 | 45 | 14 | ||
| 9 | 0 | 0 | 9 | 52 | 3 | ||
| 10 | 7 | 0 | 14 | 63 | 12 | ||
| 11 | 0 | 0 | 12 | 72 | 1 | ||
| 12 | 11 | 1 | 27 | 91 | 23 | ||
| 13 | 0 | 0 | 19 | ||||
| 14 | 11 | 0 | 29 | ||||
| 15 | 0 | 0 | 26 | ||||
| 16 | 17 | 6 | |||||
| 17 | 0 | 0 | |||||
| 18 | 15 | 1 | |||||
| 19 | 0 | 0 | |||||
| 20 | 21 | 0 | |||||
| 21 | 0 | 0 | |||||
| 22 | 19 | 1 | |||||
| 23 | 0 | 0 | |||||
| 24 | 31 | 9 | |||||
| 25 | 0 | 0 | |||||
| 26 | 26 | 1 | |||||
| 27 | 0 | 0 | |||||
| 28 | 33 | 1 | |||||
| 29 | 0 | 0 | |||||
| 30 | 34 | 1 | |||||
| 31 | 0 | 0 | |||||
| 32 | 45 | 14 | |||||
| 33 | 0 | 0 | |||||
| 34 | 37 | 1 | |||||
| 35 | 0 | 0 | |||||
| 36 | 52 | 3 | |||||
| 37 | 0 | 0 | |||||
| 38 | 49 | 3 | |||||
| 39 | 0 | 0 | |||||
| 40 | 63 | 12 | |||||
| 41 | 0 | 0 | |||||
| 42 | 64 | 4 | |||||
| 43 | 0 | 0 | |||||
| 44 | 72 | 1 | |||||
| 45 | 0 | 0 | |||||
| 46 | 70 | 1 | |||||
| 47 | 0 | 0 | |||||
| 48 | 91 | 23 |
Table of A_4n